lunes, 1 de febrero de 2016
perceptron
Introducción
Las Redes de Neuronas o Redes Neuronales, son
un paradigma de aprendizaje y procesamiento automático, inspirado en la forma
en que funciona el sistema nervioso de los animales. Se trata de un sistema de
interconexiones de neuronas que colaboran entre sí para producir una salida.
Ya que hoy en
día la IA pretende imitar la
Inteligencia natural, ya que las redes
neuronales pretenden imitar arquitectura cerebral( neuronas + conexiones) ya que
sabemos que dan inteligencia. Cabe recordar
que el termino inteligencia es bastante
antiguo, pero en este caso n el que hablamos
de redes neuronales, lo consideramos inteligencia a aquellas personas que
sabiendo de un cierto tema, son capaces
de dar una respuesta a un problema dado
como por ejemplo cálculos clasificación,
etc.
MARCO TEORICO
EL PERCEPTRÓN
La
red tipo Perceptrón fue inventada por el psicólogo Frank Rosenblatt en el año
1957. Su intención era ilustrar algunas propiedades fundamentales de los
sistemas inteligentes en general, sin entrar en mayores detalles con respecto a
condiciones específicas y desconocidas para organismos biológicos concretos.
Rosenblatt creía que la conectividad existente en las redes biológicas tiene un
elevado porcentaje de aleatoriedad, por lo que se oponía al análisis de
McCulloch Pitts en el cual se empleaba lógica simbólica para analizar
estructuras bastante idealizadas. Rosenblatt opinaba que la herramienta de
análisis más apropiada era la teoría de probabilidades, y esto lo llevó a una
teoría de separabilidad estadística que utilizaba para caracterizar las
propiedades más visibles de estas redes de interconexión ligeramente aleatorias.
El primer modelo de Perceptrón fue desarrollado en un ambiente biológico
imitando el funcionamiento del ojo humano, el fotoperceptrón como se le llamo
era un dispositivo que respondía a señales ópticas; la luz incide en los puntos
sensibles (S) de la estructura de la retina, cada punto S responde en forma
todo-nada a la luz entrante, los impulsos generados por los puntos S se
transmiten a las unidades de asociación (A) de la capa de asociación; cada
unidad A está conectada a un conjunto aleatorio de puntos S, denominados
conjunto fuente de la unidad A, y las conexiones pueden ser tanto excitatorias
como inhibitorias. Las conexiones tienen los valores posibles +1, -1 y 0,
cuando aparece un conjunto de estímulos en la retina, una unidad A se activa si
la suma de sus entradas sobrepasa algún valor umbral; si la unidad esta
activada, A produce una salida que se envía a la siguiente capa de unidades.
CARACTERÍTICAS PRINCIPALES DEL PERCEPTRON SIMPLE
- Fue introducido por Frank Rosenblatt.
- Sistema capaz de realizar tareas de clasificación de forma automática.
- A partir de un número de ejemplos etiquetados, el sistema determina la
ecuación del plano discriminante.
- Puede usarse como neurona dentro de otro tipo de red de neurona
artificial.
- Aprendizaje supervisado y conexiones en un sólo sentido.
- Es reconocido por su capacidad de aprender a reconocer patrones
- Es un modelo unidireccional compuesto por dos capas de neuronas.
- Con respecto al entrenamiento las neuronas de entrada son discretas y
la función de activación de las de salida es de tipo escalón.
ARQUITECTURA
Es una red monocapa con
varias neuronas de entrada conectadas a la neurona de salida. Observando la
imagen anterior podemos calcular el valor de la salida, del siguiente modo:
- En el caso de
que la salida sea +1, la entrada pertencerá a una clase, situada a un lado
del hiperplano
- En el caso de
que la salida sea -1, la entrada pertencerá a la clase contraria, situada
al otro lado del hiperplano
El perceptron simple es
un hiperplano de dimensión n-1 capaz de separar las clases. La ecuación de
dicho interplano es:
w1x1+w2x2+θ=0
La cual si se simplifica
queda del siguiente modo:
Donde la parte que
multiplica x1 es la
pendiente de la recta y la otra parte es el punto de corte con el eje de
ordenadas.
APRENDIZAJE SUPERVISADO
Para el proceso de
aprendizaje del Perceptron Simple es necesario saber:
- Los datos
son puntos en un espacio multidimensional.
- Se dispone
de un conjunto de observaciones, puntos representados en el hiperplano, de
los que se sabe su categoría o clase.
- Se tiene
que determinar la ecuación del hiperplano que separa los ejemplos de un
tipo de los de otro.
- La
ecuación del hiperplano se deduce a partir de los ejemplos.
- El
aprendizaje es proceso iterativo supervisado.
- Hasta
encontrar el hiperplano discriminante se debe ir modificando los
parametros de la red (pesos y umbral).
- Este
proceso de aprendizaje supervisado tiene un número finito de iteracciones.
Los pasos a seguir para
el aprendizaje son:
- Inicialización
aleatoria de los pesos y umbral.
- Se toma un
patrón de entrada-salida.
- Se calcula
la salida de la red.
- Si y =
d(x) (clasificación correcta).
Si y ≠ d(x) (clasificación incorrecta) se modifican los parámetros. - Se vuelve
al paso 2 hasta completar el conjunto de patrones de entrenamiento.
- Se repiten
los pasos anteriores hasta alcanzar el criterio de parada.
PERCEPTRON
MULTICAPA
HISTORIA
En 1969, Minsky y
Papert, demuestran que el perceptron simple y ADALINE no puede resolver
problemas no lineales (por ejemplo, XOR). La combinación de varios perceptrones
simples podría resolver ciertos problemas no lineales pero no existía un
mecanismo automático para adapatar los pesos de la capa oculta. Rumelhart y
otro autores, en 1986, presentan la "Regla Delta Generalizada" para
adaptar los pesos propagando los errores hacia atrás, es decir, propagar los
erroes hacia las capas ocultas inferiores. De esta forma se consigue trabajar
con multiples capas y con funciones de activación no lineales. Se demuestra que
el perceptron multicapa es un aproximador universal. Un perceptron multicapa
puede aproximar relaciones no lineales entre los datos de entrada y salida.
Esta red se ha convertido en una de las arquitecturas más utilizadas en el
momento.
ARQUITECTURA
Este modelo se
compone de:
- Capa de entrada: sólo
se encarga de recibir las señales de entrada y propagarla a la siguiente capa.
- Capa de salida:
proporciona al exterior la respuesta de la red para cada patrón de entrada.
- Capas ocultas:
realizan un procesamiento no lineal de los datos de entrada.
La propagación de los
patrones de entrada en el perceptron multicapa define una relación entre las
variables de entrada y variables de salida de la red. Esta relación se obtiene
propagando hacia delante los valores de entrada. Cada neurona de la red procesa
la información recibida por sus entradas y produce una respuesta o activación
que se propaga, a través de las conexiones correspondientes, a las neuronas de
la siguiente capa.
CARACTERÍSTICAS
DEL PERCEPTRON MULTICAPA.
- Es una de las
arquitecturas más utilizadas para resolver problemas reales.
- Se evalua un conjunto
de datos de entradas y se obtienen valores reales o vectores con valores
reales.
- Se diferencia del
perceptron simple y ADALINE en que tiene una capa oculta.
- Todas las neuronas se
relacionan con todas las neuroas, incluyendo las neuronas de la capa oculta.
APRENDIZAJE EN EL PERCEPTRON MULTICAPA
1. Se inicializan los
pesos y umbrales (valores aleatorios próximos a 0).
2. Se presenta un patrón
"n" de entrenamiento y se propaga hacia la salida, obteniendo la
salida de la red "y(n)"
3. Se evalúa el error
cuadrático, "e(n)", cometido por la red para cada patrón.
4. Se aplica la Regla
Delta Generalizada para modificar pesos y umbrales:
·
Se calculan los valores
"δ" para todas las neuronas de la capa de salida.
·
Se calcula "δ"
para el resto de neuronas, empezando por la última capa oculta y terminando en
la capa de entrada.
·
Se modifican los pesos y
umbrales.
5. Se repiten los pasos
2, 3 y 4 para todo el patrón de entrenamiento.
6. Se evalúa el error
total de la red.
7. Se repite hasta
alcanzar el error mínimo de entrenamiento, realizando "m" ciclos. Se
pueden establecer otros criterios de parada:
·
El error del entrenamiento
se estabilice.
·
El error de validación se
estabilice.
·
El
error de validación aumente.
CONCLUSIÓN
La Inteligencia Artificial es una rama muy importante ya que estudia
las neuronas de un ser vivo, para
desarrollar neuronales artificiales que actúan similar alas del hombre, también
cabe recalcar que el hombre
va más allá de la perfección
buscando solucionar problemas en el mundo real, atreves de las agentes
que están diseñados con neuronas artificiales, y puedan dar solución a un problema.
BIBLIOGRAFÍA
Javier, R. 2013. El perceptrón (En
linea). Consultado, 13 de enero.2016. Formato PDF. Disponible en: ftp://decsai.ugr.es/pub/usuarios/castro/Actividades/Redes-Neuronales/Apuntes/Apuntes%20Javier%20Rodriguez%20Blazquez/Redes%20de%20una%20capa.pdf
Pedro ,V e Ines , G. 2004.
Redes de neuronas
artificiales un Enfoque Práctico. 2 ed. España. Pearson Education. p 45-50.
Redes Neuronales
Introducción
- una red artificial no es nada mas y nada menos que un modelo matemático que funciona de forma de las neuronas biológicas y en la estructura diseñada para emular la forma del cerebro humano, una red artificial también puede ser vista como un sistema inteligente que lleva a cabo tareas de varias formas según su programacion y diseño. Son muy rápidas en el procesamiento de la información, existen tareas muy complejas para el ser humando que estas neuronas pueden dar facilidad y rapidez como por ejemplo el reconocimientos y clasificación de patrones que demandan demasiado tiempo y es fuerzo en las computadoras mas potente de la actualidad, cosa que el cerebro humano es mas apto para resolverlas. el cerebro puede ser considerado un sistema altamente complejo ya que su unidad básica, la neurona que esta básicamente esta masiva mente distribuida con conexiones entre ellas. En la actualidad se calcula que hay aproximadamente 10 billones de neuronas en corteza cerebral y 60 trillones de conexiones neuronales.
1.
MARCO
TEÓRICO
1.1.
REDES
NEURONALES ARTIFICIALES
Una
red neuronal artificial (ANN) es un esquema de computación distribuida
inspirada en la estructura del sistema nervioso de los seres humanos. La
arquitectura de una red neuronal es formada conectando múltiples procesadores
elementales, siendo éste un sistema adaptivo que posee un algoritmo para
ajustar sus pesos (parámetros libres) para alcanzar los requerimientos de
desempeño del problema basado en muestras representativas.
1.2.
MODELO
COMPUTACIONAL
La
diferencia entre una maquina neuronal y los programas de computador
convencional es que estas elaboran en cierta medida, la información de entrada
para obtener una salida o respuesta. No se trata de la aplicación ciega y
automática de un algoritmo.
Existen
modelos muy diversos de redes de neuronas en los cuales se siguen filosofías de
diseño, reglas de aprendizaje y funciones de construcción de las respuestas
distintas. Una primera clasificación se hace en función del recorrido que sique
la informacion dentro de la red, y así se distinguen redes alimentadas hacia
adelante y redes con retro alimentación.
1.3.
APRENDIZAJE
La
parte más importante de una red neuronal de neuronas artificiales es el
aprendizaje.
El
aprendizaje es el proceso por el cual una red neuronal modifica sus pesos en
respuesta a una información de entrada. Los cambios que se producen durante el
proceso de aprendizaje son la destrucción, modificación y creación de
conexiones entre las neuronas.
W = 0 Destrucción W › 0 Creación
Aprendizaje
El
esquema de aprendizaje de una red es lo que determina el tipo de problemas que
será capaz de resolver, l conjunto
de aprendizaje debe poseer las siguientes características:
·
Ser
significativo. Debe haber un número suficiente de
ejemplos. Si el conjunto de aprendizaje es reducido, la red no será capaz de
adaptar sus pesos de forma eficaz.
·
Ser
representativo. Los componentes del conjunto de
aprendizaje deberán ser diversos. Si un conjunto de aprendizaje tiene muchos más
ejemplos de un tipo que del resto, la red se especializara en dicho subconjunto
de datos y no será de aplicación general. Es importante que todas las regiones
significativas del espacio de estados estén suficientemente representadas en el
conjunto de aprendizaje.
El
criterio de convergencia depende del tipo de red utilizado o del tipo de
problema a resolver. La finalización del periodo de aprendizaje se puede
determinar:
·
Mediante
un número fijo de ciclos. Se decide cuantas veces
será introducido todo el conjunto, y una vez superado dicho número se detiene
el proceso y se da por aceptada la red resultante.
·
Cuando
el error descienda por debajo de una cantidad preestablecida.
En este caso habla que definir en primer lugar una función de error, bien a
nivel de patrón individual, bien a nivel de la totalidad del conjunto de entrenamiento.
Se decide a priori un valor aceptable para dicho error, y solo se para el
proceso de aprendizaje cuando la red produzca un valor de error por debajo del
prefijado. Para este criterio puede suceder que la red jamás consiga bajar por
debajo del nivel prefijado, en cuyo caso se debe disponer de un criterio
adicional de parada, por ejemplo un número de ciclos, que de utilizarse por la
red significara que esta no ha convergido. En este caso la red se dice que no
ha sido capaz de obtener una solución. Será necesario probar cambiando alguno
de los parámetros.
·
Cuando
la modificación de los pesos sea irrelevante. En
algunos modelos se define un esquema de aprendizaje que hace que las conexiones
vayan modificándose cada vez con menor intensidad. Si el proceso de aprendizaje
continuo, llegara un momento en que ya no se producirán variaciones de los
valores de los pesos de ninguna conexión; en ese momento se dice que la red ha
convergido y se detiene el proceso de aprendizaje.
Dependiendo
del esquema de aprendizaje y del problema a resolver, se pueden distinguir tres
tipos de esquemas de aprendizaje:
Aprendizaje supervisado.
En este tipo de esquemas, los datos del conjunto de aprendizaje tiene dos tipos
de atributos: los datos propiamente dichos y cierta información relativa a la
solución del problema.
·
Por ejemplo, si se trata de
definir un clasificador para u conjunto de datos, un sistema capaz de
distinguir entre caras de diferentes personas, los ejemplos contendrán datos
del individuo, una imagen de su cara, e información de la solución, de que
persona se trata (una etiqueta que la distinga). El esquema de aprendizaje
supervisado utilizara esta información para modificar las conexiones. La manera
más habitual de modificar los valores de los pesos de las conexiones es la
representada en la Figura 3.2. cada vez que un ejemplo es introducido y se
procesa para obtener una salida, dicha salida se compara con la salida que
debería haber producido, y de la que se dispone al estar incluida dicha
informacion en el conjunto de aprendizaje. La diferencia entre ambas influirá
en cómo se modificaran los pesos. Si los dos datos son muy eficientes, se
modificaran mucho los pesos si son parecidos la modificación será menor.
Para
este tipo de aprendizaje, se dice que hay un profesor externo encargado de
determinar si la red se está comportando de forma adecuada, mediante la
comparación entre la salida producida y esperada, y de actuar en consecuencia
modificando apropiadamente los valores de los pesos.
CONCLUSIÓN
se concluye este capitulo sabiendo la importancia de las redes neuronales artificiales que radica en problemas de tipo no lineal. ya que por su naturaleza experimental, por lo que por su implementacion se sustenta principalmente en métodos basados en la experiencia. sin embargo cabe recalcar que en la inteligencia artificial esta esa una de las ramas de investigación mas importante en el desarrollo y los resultados obtenidos que se obtienen hasta el momento son prometedores para el futuro.
·
ñ
BIBLIOGRAFÍA
Gómez, F; Fernández, M; López, M; Díaz, M. 2004.
Aprendizaje con redes.
Neuronas Artificiales. (En
línea). Formato PDF. Consultado el 2 de dic. 2015. Disponible en: dialnet.unirioja.es/descarga/articulo/2281678.pdf
Isasi, P; Galván, I;
2004. Redes de Neuronas Artificiales Un Enfoque Práctico.
Madrid España.
Salas, R. 2008. Redes
Neuronales Artificiales.
(En línea). Formato PDF.
Consultado el 2 de dic. 2015. Disponible en: http://www.inf.utfsm.cl/~rsalas/Pagina_Investigacion/docs/Apuntes/Redes%20Neuronales%20Artificiales.pdf
Haykin S. . Neural Networks. A Comprehensive Foundation, second edition.
Pearson Prentice
Hall, 1999
MODELO COMPUTACIONAL
1.
INTRODUCCIÓN
Para empezar debemos tener en claro
algunos conceptos básicos que
abordan los modelos computacionales.
¿Qué es un computador?
E la pregunta que muchas personas se
hacen, pero no tiene
una definición exacta, pero se
podría definir como un sistema al que se le
suministra información en forma de
datos para luego devolvernos resultados acorde a la petición del usuario,
en pocas palabras podemos decir que el
objetivo de una computadora es
básicamente resolver problemas mediantes programas. Pero ahora nos nace la pregunta.
¿Qué es un programa?
En definición
es una secuencia de instrucciones
que resuelven determinados
problemas planteados.
Al paso del tiempo el ser humano investiga
sobre las redes Neuronales
artificiales, puesto que estos
medio ofrecen una manera efectiva y eficiente
para modelar problemas que se presentan en el ámbito profesional
dando una solución más rápida al hombre
por medios de algoritmos y cálculos.
En pocas
palabras un modelo matemático en
las ciencias de la computación que
requiere extensos recursos
computacionales para
estudiar el comportamiento de un sistema
complejo por
medio de la simulación por computadora,
atreves de las redes artificiales que son
un método para resolver problemas
de una forma individual o combinada con
otros método.
3.
MARCO TEÓRICO
3.1
MODELO COMPUTACIONAL
Es un modelo matemático en
las ciencias de la computación que requiere
extensos recursos
computacionales para
estudiar el comportamiento de un sistema
complejo por
medio de la simulación por computadora. El
sistema bajo estudio es a menudo un sistema complejo no
lineal para
el cual las soluciones analíticas simples e intuitivas no están fácilmente disponibles.
En lugar de derivar una solución analítica matemática para el problema, la
experimentación es hecha con el modelo cambiando los parámetros del sistema en
la computadora, y se estudian las diferencias en el resultado de los
experimentos. Las teorías de la operación del modelo se pueden derivar/deducir
de estos experimentos de computacionales.
La gran diferencia entre una maquina conexionista, es decir una
maquina neuronal y los programas de computadoras convencionales es que
estas elaboran en ciertas medidas, la información de entrada para
obtener una salida o respuesta
Entradas =datos
Red Neuronal = procesa la información
Salida= datos
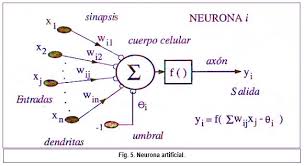
3.2 NEURONA ARTIFICIAL
·
Red neuronal biológica, cúmulo de neuronas físicamente interconectadas cuya actividad ayuda a definir un circuito reconocible en el sistema nervioso.
·
Red
neuronal artificial,
modelos matemáticos, computacionales, reales, ideales de una red neuronal
empleados en estadística, psicología cognitiva, e inteligencia artificial (Díaz, M. 2004).
Conocida como
célula o autómata, es un elemento
que posee un estado interno, llamado nivel de activación, y recibe señales
que le permiten, en su caso cambiar de
estado
Se denomina
S al conjunto de estados posibles
de la neurona, Ejemplo:
S={0,1}
Siendo
0 el estado inactive y 1 el estado
activo
Grupo de entradas x1,x2….xn son introducidas en una neurona artificial
estas entradas son definidas
por vector X, que corresponden a
una sinapsis de una neurona biológica.
Cada señal se multiplica por un peso asociado w1, w….. , wn antes de
aplicar la sumatoria etiquetado
por ∑. Cada peso corresponde a la fuerza de una conexión sináptica
es decir el nivel de concentración iónica de cada
sinapsis, y se la representa por un vector
W E=
x1w1+x2e2…+xnwn Las Señales
E son procesadas por una función llamada
de activación o salida F, que
produce la señal de salida
de la neurona S. Esto depende de cada función F, para que hayga distintos
modelos de autómatas.
3.3 Estructura de una red
Una red neuronal artificial es la interconexión de varias neuronas. El Gráfico 6 muestra una red neuronal estructurada en capas; es una de las estructuras en las cuales se pueden asociar las neuronas. En este sentido, los parámetros fundamentales de la red son: el número de capas, el número de neuronas por capa y el tipo y número de conexiones entre neuronas. No existe un método o regla que determine el número óptimo de neuronas ocultas para resolver un problema dado, generalmente se determinan por prueba y error, es decir, partiendo de una arquitectura ya entrenada, se realizan cambios aumentando y disminuyendo el número de neuronas ocultas y el número de capas, hasta conseguir la arquitectura que se ajuste a la solución del problema.
La
entrada ha sido completamente
propagada por la red, se producirá un
vector de salida, cuyos componentes son
cada uno de los valores de salida de las
células de salida.
Formulas:
Donde W1 y
W2 son
los pesos de la primera y segunda capa,
respectivamente; F es la función
de activación idéntica de todas las
neuronas; X es el vector de entrada de la red, y S es el vector de salida que produce la
red. W1 y W2 son matrices de conexiones en las capas de la red y por lo tanto esto trata de
multiplicaciones de matrices.
Lo
cual esto es equivalente a una red
con un sola capa de conexiones Wt donde
4.
CONCLUSIÓN
Bueno en pocas
palabras podemos concluir que un modelo computacional es muy útil para la ciencia de la computación. Ya que sus
procesos matemáticos son muy interesantes
para obtener una salida y conectarse
entre neuronas artificiales, dando
respuesta al vector de entrada
como un grafo cuyos nodos estos
constituidos por unidades de procesos idénticas, y que propagan
información atreves de los arcos.
BIBLIOGRAFÍA
Gómez, F; Fernández,
M; López, M; Díaz, M. 2004.
Aprendizaje con redes.
Neuronas
Artificiales. (En línea). Formato PDF.
Consultado el 2 de dic. 2015. Disponible en:
dialnet.unirioja.es/descarga/articulo/2281678.pdf
Isasi, P; Galván, I; 2004. Redes de Neuronas Artificiales Un Enfoque
Práctico.
Madrid España.
Rafael Asenjo Plaza, Eladio Gutiérrez, Julián Ramos Cózar. Fundamentos
de los Computadores”, Elementos
de Programación 1º C E. T. S. I. Universidad de Málaga / Manuales
Suscribirse a:
Entradas (Atom)